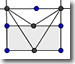
Constructing kites

Constructing kites

Image of a non-convex kite.

Did you know that there are many ways to construct a kite. An understanding of the various geometric properties allows us to understand why.

Open GeoGebra1 and investigate each of the following methods for constructing kites. Add some text to each applet to explain the following:

  1. Why does each construction give you a kite?

  2. What conditions will make it a non-convex kite2?

Circle icon Construct two intersecting circles.

Intersect icon Mark their points of intersection.

Segment icon Join each centre to each point of intersection.

Segment icon Construct a segment.

Perpendicular bisect icon Draw its perpendicular bisector.

Point icon Place two distinct points on the perpendicular bisector.

Segment icon Connect these points with the endpoints of the segment.

Polygon icon Construct two isosceles triangles sharing a common base.

Note: Make sure you have two distinct third vertices.

Midpoint icon In a rectangle, mark the midpoints of two opposite sides.

Parallel icon Draw a line parallel to those two chosen sides.

Intersect icon Mark the points of intersection of the other two sides (or their extensions) and the parallel line you have drawn.

Segment icon Connect those intersection points to the given midpoints.

reflect icon Reflect any triangle over any one of its sides.

Note: Click on the triangle, then the side.

Links

  1. https://www.geogebra.org/
  2. https://en.wikipedia.org/wiki/Convex_set